Объяснение алгоритма Page Rank

2. Сложный

PageRank - это семейство алгоритмов для назначения числовых весов для документов с гиперссылками (или веб-страниц), проиндексированных поисковый движок , Его свойства много обсуждаются поисковая оптимизация (SEO) эксперты. Система PageRank используется популярными поисковый движок Google, чтобы помочь определить релевантность или важность страницы. Он был разработан основателями Google Ларри Пейджем и Сергеем Брином в Стэнфордском университете в 1998 году. Как говорит Google ( http://www.google.com/technology/ ):

PageRank опирается на уникальную демократичность сети, используя ее обширную структуру ссылок в качестве показателя ценности отдельной страницы. Google интерпретирует ссылку со страницы A на страницу B как голосование, за страницу A, за страницу B. Но Google смотрит больше, чем просто количество голосов, или ссылки, которые получает страница; он также анализирует страницу, которая голосует. Голоса, поданные на страницах, которые сами по себе "важны", весят больше и помогают сделать другие страницы "важными".

Другими словами, рейтинг страницы является результатом «голосования» среди всех других страниц в World Wide Web о том, насколько важна страница. Гиперссылка на страницу считается голосованием поддержки. PageRank страницы определяется рекурсивно и зависит от числа и метрики PageRank всех страниц, которые ссылаются на нее («входящих ссылок»). Страница, которая связана многими страницами с высоким рейтингом, сама получает высокий рейтинг. Если нет ссылок на веб-страницу, эта конкретная страница не поддерживается. Панель инструментов Google PageRank изменяется от 0 до 10. Кажется, что это логарифмическая шкала. Точные детали этой шкалы неизвестны.

Название PageRank является товарным знаком Google. Был ли каламбур на имени Ларри Пейджа и на слове «страница» преднамеренным или случайным, остается открытым вопросом. Процесс PageRank был запатентован (патент США № 6285999 ( http://patft.uspto.gov/netacgi/nph-Parser?Sect1=PTO1&Sect2=HITOFF&d=PALL&p=1&u=/netahtml/srchnum.htm&r=1&f=s&l=50 6 285 999.WKU. & OS = PN / 6 285 999 и RS = PN / 6 285 999 )).

Альтернативой алгоритму Page rank, предложенному Джоном Клейнбергом, является алгоритм HITS.

Алгоритм ранжирования страниц

упрощенный

Предположим, что небольшая вселенная состоит из четырех веб-страниц: A , B , C и D. Если все эти страницы ссылаются на A , то PR (PageRank) страницы A будет суммой PR страниц B , C и D.

PR ( A ) = PR ( B ) + PR ( C ) + PR ( D )

Но тогда предположим, что страница B также имеет ссылку на страницу C , а страница D содержит ссылки на все три страницы. Никто не может голосовать дважды, и по этой причине считается, что страница B дала половину голоса каждому. По той же логике, только одна треть голосов D засчитывается за PageRank.

Другими словами, разделите PR на общее количество ссылок, которые приходят со страницы.

Наконец, все это уменьшается на определенный процент путем умножения его на коэффициент q . По причинам, изложенным ниже, ни одна страница не может иметь PageRank, равный 0. Таким образом, Google выполняет математическую операцию и дает каждому минимум 1 - q . Это означает, что если вы уменьшите всех на 15%, вы вернете им 0,15.

Таким образом, PageRank одной страницы рассчитывается по PageRank других страниц. Google всегда пересчитывает PageRanks. Если вы дадите всем страницам PageRank любого числа (кроме 0) и будете постоянно пересчитывать все, все PageRank изменится и будет стабилизироваться в какой-то момент. Именно в этот момент PageRank используется поисковой системой.

Сложный

В формуле используется модель случайного пользователя, который скучает после нескольких нажатий и переключается на случайную страницу. Значение PageRank страницы отражает частоту посещений этой страницы случайным пользователем. Его можно понимать как марковский процесс, в котором состояния являются страницами, и все переходы одинаково вероятны и являются связями между страницами. Если страница не имеет ссылок на другие страницы, она становится приемником и, следовательно, делает эту вещь непригодной для использования, потому что приемные страницы навсегда задержат случайных посетителей. Однако решение довольно простое. Если случайный пользователь переходит на страницу-приемник, он выбирает другой URL-адрес случайным образом и продолжает просмотр.

Чтобы быть справедливым со страницами, которые не являются приемниками, эти случайные переходы добавляются ко всем узлам в Интернете с остаточной вероятностью, обычно равной q = 0,15, оцениваемой по частоте того, что средний серфер использует закладку своего браузера.

Итак, уравнение выглядит следующим образом:

где p 1, p 2, ..., p N - рассматриваемые страницы, L ( p i ) - набор страниц, ссылающихся на p i , а N - общее количество страниц.

Значения PageRank являются записями доминирующего собственного вектора модифицированной матрицы смежности. Это делает PageRank особенно элегантной метрикой: собственный вектор

где R - решение уравнения

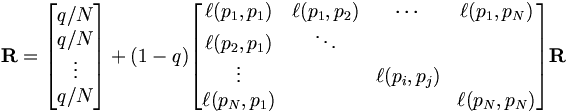
где функция смежности 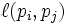равно 0, если страница p i не связана с p j , и нормализована так, что для каждого i

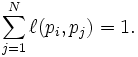
Значения собственного вектора PageRank быстро приближаются (требуется всего несколько итераций), и на практике это дает хорошие результаты.

В результате теории Маркова можно показать, что PageRank страницы - это вероятность оказаться на этой странице после большого количества кликов. Это происходит равным t - 1, где t - это ожидаемое количество кликов (или случайных скачков), необходимое для того, чтобы получить страницу обратно к себе.

Основным недостатком является то, что он предпочитает старые страницы, потому что новая страница, даже очень хорошая, не будет иметь много ссылок, если она не является частью существующего сайта (сайт представляет собой плотно связанный набор страниц).

Вот почему PageRank следует сочетать с текстовым анализом или другими методами ранжирования. PageRank, кажется, предпочитает страницы Википедии, часто ставя их высоко или в верхней части поисков по нескольким энциклопедическим темам. Общепринятая теория заключается в том, что это связано с тем, что Википедия тесно взаимосвязана: каждая статья имеет множество внутренних ссылок из других статей, которые, в свою очередь, содержат ссылки со многих других сайтов в Интернете, указывающие на них. По сравнению с Википедией и подобными высококачественными сайтами с высоким содержанием контента остальная часть Всемирной паутины относительно слабо связана.

Тем не менее, Google, как известно, активно наказывать ссылки фермы и другие схемы искусственного раздувания PageRank. То, как Google показывает разницу между сильно взаимосвязанными веб-сайтами и ссылочными фермами, является его коммерческой тайной.

!!! Эта статья лицензирована под GNU Free Documentation License, что означает, что вы можете копировать и изменять ее, пока вся работа (включая дополнения) остается под этой лицензией. Увидеть http://www.gnu.org/copyleft/fdl.html для деталей. Он использует материал из статьи Википедии PageRank !!!

Похожие

Комментарии